
Американские физики из Колорадского университета в Болдере, Национального института стандартов и технологии (NIST) и их общего исследовательского центра JILA опубликовали новую оценку максимального значения величины электрического дипольного момента (ЭДМ) электрона. Точность удалось повысить на порядок, и теперь оценка составляет (−1,3±2,0±0,6)×10−30 e·см с учетом погрешностей. Эта информация потенциально представляет большой интерес как для физики элементарных частиц, так и для современной теории происхождения Вселенной.
Минипроекты для большой физики
Исследования, о которых пойдет речь, восстанавливают весьма почтенную традицию камерных экспериментов в физике микромира, которая господствовала на протяжении конца XIX столетия и весьма значительной части столетия двадцатого. Чтобы оценить ее по достоинству, углубимся в не столь уж далекую историю.
Физика частиц родилась вместе с фактически случайным наблюдением радиоактивности урана членом Французской академии наук Антуаном Анри Беккерелем в феврале 1896 года. Уже на следующий год Джозеф Джон Томсон после интенсивных поисков открыл первую элементарную частицу, электрон, а потом, как говорится, пошло-поехало. В 1899 году перебравшийся в Монреаль бывший сотрудник Томсона двадцатипятилетний уроженец Новой Зеландии Эрнест Резерфорд обнаружил, что уран испускает два вида частиц (или, как тогда говорили, эманации), которые он назвал альфа- и бета-лучами. Природа бета-лучей выяснилась в том же году, когда Фриц Гейзель, Беккерель и Мария Склодовская-Кюри пришли к заключению, что это просто быстрые электроны. Проблему альфа-частиц в основном разрешил сам Резерфорд в счастливом для себя 1908 году, принесшем ему Нобелевскую премию по химии. Он доказал, что там, где присутствует источник альфа-излучения, появляются атомы гелия (сейчас даже школьник знает, что альфа-частицы — это ядра гелия-4, но тогда понятия атомного ядра просто не существовало). А в интервале между этими событиями, в первый год XX века, француз Поль Виллар открыл у урана еще один вид излучения, которое тот же Резерфорд обозначил третьей буквой греческой алфавита — гаммой. В 1910 году английский физик Уильям Генри Брэгг доказал, что гамма-лучи представляют собой электромагнитные волны очень малой длины.
Об истории физики частиц можно писать до бесконечности, но сейчас я хотел бы выделить в ней очень интересный тренд. Приблизительно до конца 1930-х годов исследования в этой области осуществлялись, как говорится, на лабораторных столах (открытие частиц в космических лучах — это особая статья, которой я не касаюсь). Такими были, в частности, исторические эксперименты Резерфорда и его ассистентов Эрнеста Марсдена и Иоганнеса Гейгера по бомбардировке альфа-частицами мишеней из золотой фольги, результаты которых в 1911 году привели Резерфорда к планетарной модели атома. Такими были и прочие фундаментальные достижения этой науки — скажем, открытие нейтрона Джеймсом Чедвиком в 1932 году (а также «почти» открытие той же частицы Фредериком и Ирен Жолио-Кюри, которые имели полный набор релевантных экспериментальных данных, но не смогли его правильно осмыслить, равно как и последующее открытие ими же искусственной радиоактивности). Наконец, таким же было и открытие деления ядер урана под действием нейтронного облучения, сделанное в 1938 году в берлинском Институте химии общества кайзера Вильгельма его тогдашним директором профессором Отто Ганом и его ассистентом Фрицем Штрассманом.
Как известно, ядерную физику и физику частиц (в 1930-е годы это была практически одна и та же сфера исследований) революционизировало изобретение циклического резонансного ускорителя протонов, сделанное в 1930 году американскими физиками Эрнестом Орландо Лоуренсом и Милтоном Стэнли Ливингстоном. Однако и эти замечательные машины поначалу опять-таки вполне умещались (или могли умещаться) на лабораторных столах. Первый демонстрационный циклотрон Лоуренса и Ливингстона имел в диаметре около 10 см, второй — 25 см, третий (а это уже была вполне серьезная машина, разгонявшая протоны до энергии 5 МэВ) — 69 см. Первый европейский циклотрон, запущенный в 1937 году в ленинградском Радиевом институте, был всего лишь метрового диаметра и при этом на 20% уступал в энергии протонного пучка третьей версии циклотрона Лоуренса. В общем, вплоть до начала Второй мировой войны эксперименты в этой области науки оставались вполне маломасштабными.

Размеры циклических ускорителей заряженных частиц резко выросли после открытия принципа автофазировки, сделанного советскими физиками Владимиром Векслером и Евгением Фейнбергом и американцем Эдвином Макмилланом. После этого уже в 1950-е годы были сконструированы и построены различные версии ускорителей-гигантов. Первую такую машину с вакуумной камерой 23-метрового диаметра, названную Космотроном, в 1952 году запустили в Брукхейвенской национальной лаборатории в штате Нью-Йорк. Сначала она ускоряла протоны до энергии 2,3 ГэВ, а после окончательной доводки — до 3,3 ГэВ. В 1954 году заработал ускоритель в университете Беркли, который годом позже вышел на энергию 6,2 ГэВ, позволившую рождать антипротоны и антинейтроны. В 1957 году в Дубне запустили синхрофазотрон на 10 ГэВ. Потом без большой задержки стали появляться еще более мощные (и, соответственно, более крупные) циклические и линейные ускорители протонов, ионов и электронов, на которых было сделано множество замечательных открытий.
И дело было не только в ускорителях. Например, экспериментальная установка, на которой американские физики Фредерик Райнес и Клайд Коуэн (Clyde Cowan) в 1956 году впервые детектировали нейтрино, весила около десяти тонн. К слову, позднейшие нейтринные детекторы, включая и знаменитый антарктический нейтринный телескоп IceCube, отличались и отличаются куда большими масштабами. В общем, уже в середине 1950-х годов вполне могло показаться, что эпоха камерных экспериментов в физике частиц ушла в прошлое и вряд ли вернется.
Однако даже тогда подобный прогноз был бы неверен. Вероятно, самым фундаментальным достижением этого десятилетия в физике частиц стал в полном смысле слова исторический эксперимент, выполненный в 1956 году профессором Колумбийского университета Ву Цзяньсюн (к слову, первой женщиной, избранной президентом Американского физического общества) вместе с Эрнестом Эмблером (Ernest Ambler) и тремя его коллегами по вашингтонскому Национальному бюро стандартов. Они проверили и подтвердили парадоксальную с точки зрения тогдашней науки гипотезу, которую чуть ранее выдвинули работавшие в США соотечественники профессора Ву физики-теоретики Ли Цзундао и Янг Чженьнин. Они предположили, что в актах бета-распада атомных ядер (как и в других превращениях, обусловленных слабым взаимодействием) может нарушаться считавшийся незыблемым закон сохранения пространственной четности, который в 1927 году сформулировал замечательный венгерский физик и будущий нобелевский лауреат Юджин Вигнер. Несоблюдение этого закона означает, что природа в определенных ситуациях делает различия между физическими процессами и их зеркальными отражениями — или, что то же самое, между правым и левым. Согласно гипотезе Ли и Янга, такие различия проявляются только в процессах, управляемых слабым взаимодействием (в остальных трех фундаментальных взаимодействиях — сильном, электромагнитном и гравитационном — пространственная четность сохраняется).
Профессор Ву и ее коллеги поставили очень изящный (а по идее даже простой) эксперимент, поместив образец с бета-радиоактивным изотопом кобальта-60 в однородное магнитное поле, которое ориентировало спины (и, следовательно, магнитные моменты) ядер кобальта преимущественно в одном направлении. Если бы пространственная четность оставалась ненарушенной, ядра кобальта в актах бета-распада испускали бы электроны с равной интенсивностью как в сторону своих спинов, так и в противоположном направлении. Однако эксперимент показал сильную пространственную асимметрию распада — антипаралельно ориентации спинов вылетало приблизительно на 40% больше электронов, нежели в обратную сторону.
Для подавления теплового разброса ориентации ядерных спинов эксперимент проводился в криостате при температуре около одной сотой кельвина, и этот криостат приблизительно метрового размера стал самой объемной частью всей установки. Так что исключительно важный результат группы Ву и Эмблера был получен в ходе чисто камерного эксперимента. То же самое можно сказать о результатах американских физиков, которые будут обсуждаться в этой статье. Но для понимания их цели и смысла нам понадобится дополнительная информация из физики элементарных частиц.P-, C-, CP- и CPT-симметрии
Я рассказал об эксперименте группы Ву отнюдь не случайно. Дело в том, что интерес ряда физиков к измерению электрического дипольного момента (ЭДМ) электрона восходит как раз к доказательству несохранения четности в слабых взаимодействиях — правда, в довольно глубокой ретроспективе.
Когда специалисты по физике частиц узнали о результатах эксперимента Ву и ее коллег (и аналогичного по выводам, но осуществленного другим способом эксперимента, выполненного в 1957 году под руководством Леона Ледермана), они испытали довольно сильный шок. Однако без большой задержки Ли и Янг в США и Лев Давидович Ландау в СССР высказали гипотезу, что любые физические взаимодействия (следовательно, и слабое) инвариантны относительно произведения (композиции) двух операций — зеркального отражения (его принято обозначать латинской буквой P) и зарядового сопряжения, то есть замены частиц на античастицы (операция C). Это означает, что две системы частиц, одна из которых получается из другой применением этих операций, будут физически эквивалентны. Согласно гипотезе Ли, Янга и Ландау, эта так называемая CP-симметрия сохраняется во всех элементарных процессах. Поэтому, например, распад частиц под действием слабого взаимодействия должен выглядеть точно так же, как отраженный в зеркале распад их античастиц.
Однако эта красивая гипотеза продержалась недолго. В 1964 году американские физики во главе с Джеймсом Кронином и Валом Фитчем экспериментально доказали, что CP-симметрия не соблюдается при распадах некоторых электрически нейтральных каонов (они же К-мезоны). Так, ее сохранение запрещало каону \(K_2^0\) распадаться на два нейтральных пиона — только на три. Однако Кронин, Фитч и их коллеги обнаружили, что приблизительно 0,2% таких распадов все же приходится на пионные пары. Хотя это нарушение СР-симметрии было очень незначительным, оно все же имело место.
И здесь история не закончилась. В самом начале нашего столетия японские и американские физики выяснили, что эта симметрия не соблюдается и при распадах нейтральных B-мезонов, причем куда сильнее, чем в случае каонов. Я не буду вдаваться в подробности этих экспериментов, вот хороший обзор. Главное в том, что в природе существуют процессы с участием слабого взаимодействия, которые нарушают СР-симметрию (кстати, в них также участвуют и нейтральные D-мезоны). Иначе говоря, эта симметрия не универсальна.
Как зеркальное отражение, так и зарядовое сопряжение относятся к числу дискретных преобразований, не зависящих ни от каких численных параметров. Напротив, лежащие в основе эйнштейновской теории относительности преобразования группы Лоренца непрерывны, поскольку зависят от относительной скорости систем отсчета. В квантовой физике имеется еще одно важнейшее дискретное преобразование T — обращение времени. Подобно двум другим, оно влияет на поведение различных физических величин. Например, при обращении времени энергия частицы (или системы частиц) сохраняется, импульс и угловой момент (как орбитальный, так и спиновый) меняют знаки на противоположные, электрическое поле остается неизменным, а магнитное поле опять-таки меняет знак.
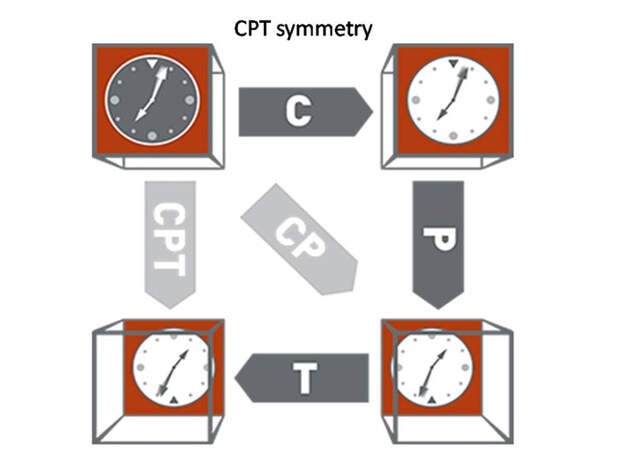
Можно подумать, что обращение времени, в отличие от операций С и Р, есть чисто математическая процедура, ведь в реальности оно не наблюдается. Его можно имитировать, прокрутив вспять киноленту, но к физике такой фокус отношения не имеет. На деле ситуация сложнее. В первой половине 1950-х годов несколько физиков (включая таких гигантов, как Джулиан Швингер и Вольфганг Паули) разными способами и с разной убедительностью доказали чрезвычайно важный принцип, получивший название CPT-теоремы. Она утверждает, что любая квантовополевая теория, удовлетворяющая требованию лоренц-ковариантности и еще паре-тройке абсолютно разумных ограничений, должна быть инвариантна относительно последовательного применения операций C, P и T (в любом порядке). Это означает, что если взять любую теорию из этого семейства и подвергнуть ее уравнения операциям зеркального отражения, замены частиц на античастицы и обращения времени, то вторая теория будет физически эквивалентна первой. У CPT-теоремы есть немало очень глубоких следствий: например, из нее вытекает, что массы и времена жизни любой частицы и ее античастицы должны быть абсолютно одинаковы. Пока что ни один эксперимент не поставил этот вывод под сомнение.
А вот и еще одно следствие. Если CPT-теорема верна, а CP-инвариантность хоть где-то нарушается, то не должна соблюдаться и T-инвариантность. Так что выходит, что в каких-то превращениях частиц нарушается обратимость времени! Физически это означает, что скорость таких превращений в «прямом» и «обратном» направлениях неодинакова. Выходит, что в микромире есть своя стрела времени. В прошлом столетии этот открытие стало крупной неожиданностью для физиков.
В этом не было бы ничего удивительного, если бы мы говорили о макропроцессах, которые описываются классической физикой. Так, обратимость времени несовместима со вторым законом термодинамики, который утверждает, что в макромире все реальные процессы должны идти с суммарным возрастанием энтропии. Это, конечно, понятно и без высокой науки — налитый из чайника кипяток постепенно остывает, но сам собой никогда не нагревается. Однако тот факт, что в микромире тоже есть стрела времени, стал для физиков крупной неожиданностью.
Но и это не всё. Нарушения СР-симметрии непосредственно связаны с отличием материи от антиматерии. Об этом говорит очень красивый эксперимент с нейтральными каонами, выполненный в ЦЕРНе в конце 1990-х годов, который стоит вспомнить, пусть и без подробностей.
Для начала отмечу, что если бы СР-симметрия соблюдалась абсолютно строго, то нейтральные каоны переходили бы в свои античастицы с точно такой же вероятностью, с какой те претерпевали бы обратные превращения. Любое нарушение СР-симметрии должно влечь за собой изменение одной из этих вероятностей. Если приготовить пучок из равного числа нейтральных каонов и антикаонов и проследить динамику концентрации тех и других, можно выяснить, уважают ли их превращения СР-симметрию.
Именно это и сделали физики из ЦЕРН. Они выяснили, что нейтральные антикаоны становятся каонами чуть-чуть быстрее, чем те превращаются в антикаоны. Иначе говоря, был обнаружен процесс, в ходе которого антиматерия превращается в материю быстрее, чем материя — в антиматерию! В смеси с изначально равными долями вещества и антивещества со временем образуется пусть небольшой, но все же поддающийся измерению избыток вещества. Такой же эффект был выявлен в экспериментах и с другими массивными нейтральными частицами — уже упоминавшимися D0-мезонами иB0-мезонами.
Таким образом, к концу ХХ века экспериментаторы убедительно доказали, что слабые взаимодействия по-разному влияют на частицы и античастицы. Хотя эти различия сами по себе очень малы и выявляются лишь в ходе некоторых превращений весьма экзотических частиц, они демонстрируют физическую асимметрию между материей и антиматерией. Это означает, что природа на фундаментальном уровне не соблюдает и С-симметрию.
Эти результаты имеют прямое отношение к космологии. Астрофизики давно установили, что в современной Вселенной нет областей, заполненных антивеществом со времени ее рождения. Конечно, античастицы разных видов постоянно возникают (и аннигилируют) в великом множестве высокоэнергетичных процессов (например, в звездных ядрах), но погоды они не делают. Речь идет о полном отсутствии реликтового антивещества, оставшегося с самой ранней эпохи существования Вселенной. Поскольку ядра всех элементов Периодической системы, которые и образуют «обычное» вещество, состоят из барионов (конкретно, из протонов и нейтронов), это положение дел несколько условно называют барионной асимметрией Вселенной. Коль скоро барионы состоят из кварков, можно было бы говорить и о кварковой асимметрии. Частицы темной материи, если они существуют, в этот расклад не входят, поскольку их природа не известна.
Барионная асимметрия нуждается в разумном объяснении. Конечно, можно допустить, что Вселенная с самого рождения вообще не содержала антивещества, но поверить в это трудно. Куда естественней предположить, что самая ранняя (и чрезвычайно горячая и плотная) Вселенная была в равной мере заполнена частицами и античастицами. Однако потом — и очень быстро — возник небольшой избыток частиц. Поскольку плотность материи была в то время исключительно высока, все античастицы встретились с частицами и аннигилировали, а выжившие частицы дали начало всем видам вещества. Этот гипотетический процесс называют генерацией барионной асимметрии.
В 1967 году Андрей Дмитриевич Сахаров опубликовал ставшую классической статью, в которой сформулировал три условия, необходимые для генерации барионной асимметрии (А. Д. Сахаров, 1967. Нарушение СР-инвариантности, С-асимметрия и барионная асимметрия Вселенной). И одно из них как раз требует того самого нарушения С-симметрии и СР-симметрии, о котором говорилось выше. Его физический смысл совершенно ясен. Если бы бы такого нарушения не было, то процессы с участием кварков и антикварков происходили бы с одинаковой скоростью, и изначально барион-симметричная среда такой бы и осталась на все времена.
Казалось бы, все в порядке, причина барионной асимметрии найдена. Но — так, да не так. Во-первых, нарушение этих двух симметрий выявлено в экспериментах, охватывающих один лишь кварковый сектор материи. К тому же оно затрагивает лишь процессы с участием кварков только двух старших поколений — странных, очарованных и b-кварков. Кварки первого поколения, из которых состоят протоны и нейтроны, остались вне игры. Во-вторых, масштабы этих нарушений слишком малы, чтобы ими можно было объяснить генерацию барионной асимметрии. И дело не только в экспериментах с экзотическими мезонами. Господствующая сейчас теория микромира, Стандартная модель элементарных частиц, тоже допускает процессы с нарушением дискретных симметрий — но опять-таки, в слишком незначительных масштабах. Так что проблема остается.
В общем, вывод ясен. Физика нуждается в более убедительных объяснениях барионной асимметрии, и лучше бы их нашлось побольше. Теоретики, конечно, таковые уже придумали, но и новые не помешают. В частности, такие резервные варианты стоит поискать не в кварковом, а в лептонном секторе.
Наконец-то ЭДМ
После столь длинного введения можно наконец-то перейти к статье физиков из Колорадского университета в Болдере. Как уже говорилось, они заново оценили максимальную величину электрического дипольного момента (ЭДМ) самой известной и самой изученной элементарной частицы — электрона. Эта информация имеет непосредственное отношение к нарушению дискретных симметрий, о котором говорилось в предыдущем разделе.
ЭДМ любой физической системы, содержащей электрически заряженные компоненты (дискретные или непрерывно распределенные в ее объеме) — это векторная величина, которая в первом приближении характеризует пространственную структуру всей совокупности этих компонент. Я не буду приводить формальных определений, их можно найти, например, здесь. Если считать электрон чем-то вроде микросферы, равномерно заполненной отрицательным электричеством, ее ЭДМ окажется строго нулевым. С другой стороны, если рассматривать электрон как некое подобие овала с переменной плотностью распределения заряда, то его ЭДМ в общем случае будет отличен от нуля. При этом его направление (напомню, что ЭДМ — это вектор) всегда должно быть коллинеарно (то есть параллельно или антипараллельно) спину электрона. Причина этого проста: спин электрона — это его единственный собственный параметр, который может ориентироваться в пространстве и тем самым задавать определенное направление. Кстати, это же верно и в отношении магнитного дипольного момента, который тоже коллинеарен спину (точнее, антипараллелен — в силу того, что заряд электрона считается отрицательным).
Откуда у электрона мог бы появиться ЭДМ? Согласно Стандартной модели, это может произойти в силу взаимодействия электрона с массивными частицами, которое не будет обладать ни СР-инвариантностью, ни, соответственно, С-инвариантностью. В результате оно сможет вызвать перераспределение плотности электронного заряда и тем самым породить электронный ЭДМ. Единица измерения ЭДМ электрона или любой другой частицы — это произведение элементарного электрического заряда e (который по определению считается положительным и равен 1,6×10−19 кулона) на сантиметр. Согласно Стандартной модели, электронный ЭДМ по порядку величины никак не может превышать 10−38 e·см. Прямое измерение столь малой величины пока лежит за рамками возможностей эксперимента.
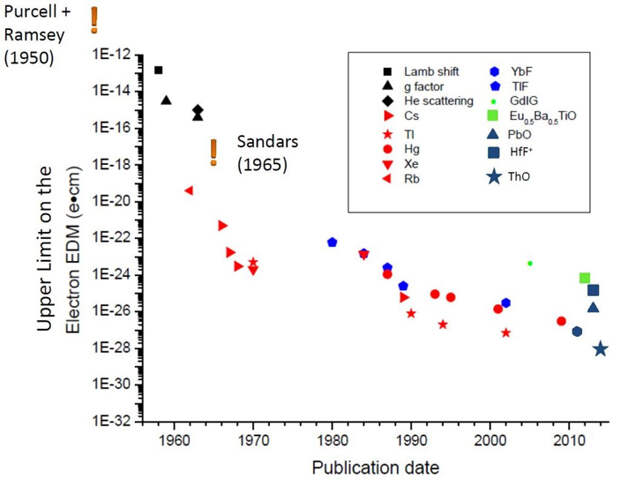
Казалось бы, при таком раскладе зачем и стараться? Однако можно предположить, что существуют лежащие за рамками Стандартной модели частицы, которые порождают у электрона ЭДМ куда большей величины. И это отнюдь не произвольная фантазия. Некоторые расширения Стандартной модели (в частности, основанные на теории суперструн) дают для ЭДМ электрона значения, лежащие в диапазоне (10−27–10−30) e·см. Такие величины уже доступны для измерения в современных прецизионных экспериментах. Если бы их удалось определить, можно было бы приблизительно установить и массу этих гипотетических частиц, которая во многих моделях обратно пропорциональна квадратному корню из абсолютной величины электронного ЭДМ. А после этого имело бы смысл задуматься и о возможности (либо невозможности) их детектирования на БАК или более мощных ускорителях, которые, как надеются физики, когда-нибудь придут ему на смену. Главная надежда состоит в том, что такие частицы могли бы увеличить степень нарушения С- и СР-инвариантности в слабых взаимодействиях и тем самым помочь решить проблему барионной асимметрии.
Не надо думать, что интерес к электронному ЭДМ возник лишь недавно. Физики начали обдумывать эту проблему свыше сорока лет назад, вскоре после создания Стандартной модели. Однако первая экспериментальная оценка этой величины, полученная гарвардско-йельской коллаборацией ACME (Advanced Cold Molecule Electron), которая по порядку величины не слишком отличается от новейшего результата физиков из Болдера, была опубликована только в конце 2013 года (см. новость Первые результаты эксперимента ACME: электрический дипольный момент электрона по-прежнему нулевой, «Элементы», 30.12.2013). Согласно выводам ее участников, абсолютная величина электронного ЭДМ не может превышать 8×10−29 e·см. Как видим, этот верхний предел укладывается в отмеченный в предшествующем абзаце диапазон возможных значений ЭДМ в ряде расширенных версий Стандартной модели.
Один из возможных путей к измерению электронного ЭДМ по идее очень прост. Возьмем молекулу, имеющую достаточно автономный валентный электрон и сильное внутреннее электрическое поле, задающее ее геометрическую ось. Затем найдем способ ориентировать спин валентного электрона параллельно и антипараллельно этому полю. Если ЭДМ электрона равен нулю, оба состояния молекулы будут иметь одинаковую энергию. При ненулевом ЭДМ его вектор также будет менять ориентацию относительно поля, и между энергетическими уровнями этих состояний появится различие. Если его удастся измерить, можно будет определить и величину ЭДМ (естественно, работать надо не с одной молекулой, а с целым молекулярным ансамблем). Именно такова схема эксперимента коллаборации ACME, которая использовала молекулы монооксида тория ThO.
Физики из Болдера применили тот же метод, но в другом исполнении. Вместо оксида тория они работали с однократно ионизированными молекулами фторида гафния HfF+. Эти молекулы обладают чрезвычайно сильным внутренним электрическим полем с эффективной напряженностью 23 гигавольт/см, направленным от иона гафния к иону фтора. Вектор этого поля как раз и задает геометрическую ось каждой молекулы.
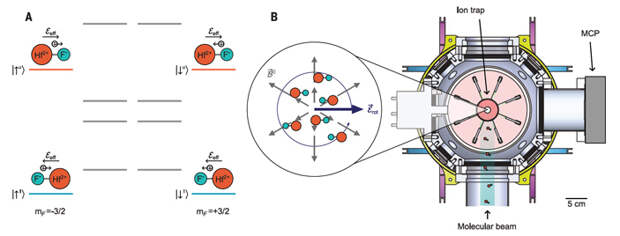
Общая схема эксперимента представлена на рисунке ниже. Заряженные молекулы фторида гафния «запирались» в ионной ловушке, на которую накладывалось вращающееся внешнее электрическое поле напряженностью около 58 вольт/см. Под его воздействием молекулы переходили в серию дублетных состояний (см. Doublet state). При этом у двух таких дублетов молекулярные оси оказывались ориентированы в пространстве — у одного параллельно внешнему полю (он изображен в верхней части схемы), у другого антипараллельно (нижняя часть). Дополнительно на ловушку накладывалось слабое магнитное поле, которое действовало на магнитные моменты валентных электронов. В результате у одних молекул каждого дублета спины этих электронов ориентировались более или менее в направлении внутримолекулярного электрического поля, а у других обретали противоположную ориентацию (направления спинов также представлены на схеме). Благодаря этому состояния с разными спиновыми ориентациями валентного электрона могли оказываться на разных энергетических уровнях — естественно, только если электронный ЭДМ отличен от нуля. В этом случае у обоих дублетов разница между уровнями должна равняться удвоенному произведению абсолютной величины ЭДМ на напряженность внутримолекулярного поля — у одного со знаком плюс, а у другого со знаком минус. На правой половине рисунка представлена схема ионной ловушки, в которой проводились измерения. Поскольку там задан и масштаб, хорошо видно, что размеры ловушки измеряются всего лишь десятками сантиметров. Так что это вполне камерный эксперимент.
Экспериментаторы предполагали, что в силу огромной величины внутримолекулярного поля (напомню, аж 23 ГВ/см!), такие различия в энергии удастся обнаружить даже при очень малой величине электронного ЭДМ. Соответствующие измерения проводились на пространственно разделенных «облаках» молекул, которые приготовлялись в том или ином дублетном состоянии. Эксперимент продолжался около двух месяцев, а суммарное время измерений составило около 620 часов. Он был осуществлен в 1370 раундах, причем для каждого использовалось порядка двадцати тысяч ионов фторида гафния. Технические детали измерений подробно описаны в обсуждаемой статье.

Физики из Болдера впервые опробовали свой метод еще 6 лет назад, но их тогдашние результаты оказались довольно грубыми и заведомо уступали по надежности результатам коллаборации ACME (W. Cairncross et al., 2017. Precision Measurement of the Electron’s Electric Dipole Moment Using Trapped Molecular Ions). Последующая отработка экспериментальной техники позволила их заметно улучшить. Теперешняя оценка величины электронного ЭДМ равна (−1,3±2,0±0,6)×10−30 e·см. Первая поправка представляет статистическую погрешность обработки экспериментальных данных, а вторая — систематическую погрешность. Знак «минус» перед значением ЭДМ означает, что он направлен антипараллельно спину электрона.
Окончательный вывод участников эксперимента состоит в том, что абсолютное значение верхней границы величины электрического дипольного момента электрона с 90-процентой достоверностью равно 4,1×10−30 e·см. Если предположить, что этот момент действительно отличен от нуля и создан «вмешательством» еще неизвестных массивных частиц, то, согласно упоминавшимся расширениям Счтандартной модели, их масса не может быть меньше 40 ТэВ. Поскольку максимальная энергия протон-протонных столкновений на Большом адронном коллайдере сейчас равна 13,6 ТэВ, получение этих частиц на БАК пока что неосуществимо. По всей вероятности, в ближайшие десять лет эта ситуация не изменится.
А вот попытки измерить величину электронного ЭДМ они практически наверняка будут продолжаться, причем разными способами. Стоят они сравнительно немного (особенно в сравнении с затратами на суперускорители), а результаты могут дать весьма интересные. О планах будущих экспериментов этого рода, которые сейчас прорабатываются, рассказано в конце заметки, опубликованной в том же выпуске Science, что и статья физиков из Болдера. А пока что стоит набраться терпения.
А в заключение вишенка на торте. В Северо-Западном университете, расположенном в пригороде Чикаго Эванстоне, уже несколько лет действует Центр исследований в области фундаментальной физики посредством настольных экспериментов (Center for Fundamental Physics with Tabletop Experiments). Там очень активно развивают новые технологии суперпрецезионных измерений, которые обещают открыть новые тайны микромира. Я думаю, что стоит последить за его работой.
Источник: Tanya S. Roussy, Luke Caldwell, Trevor Wright, William B. Cairncross, Yuval Shagam, Kia Boon Ng, Noah Schlossberger, Sun Yool Park, Anzhou Wang, Jun Ye, Eric A. Cornell. An improved bound on the electron’s electric dipole moment // Science. 2023. DOI: 10.1126/science.adg4084.
Алексей Левин

Свежие комментарии